本文作者才疏学浅，许多概念也是在写本文的过程中学习的，如有疏漏纰谬等等，不胜惶恐，多请读者指正

i. 悖论

一直到19世纪末期为止，用于描述数学的语言都是相当不精确的，有时候，人们想要指代“一个单独的对象”，而有的时候，人们则想要指代“一组对象”。在彼时，这两者之间并没有什么形式上的区别，人们只会用自然语言来结合上下语境来描述自己想要的东西——这一情形一直持续到格奥尔格·康托尔(Georg Cantor)发明朴素集合论（Naïve Set Theory）为止，在朴素集合论被发表后，伯特兰·罗素(Bertrand Russell)发现了关于朴素集合论的一个悖论，这个悖论源于朴素集合论中对于集合（Set）的构造的处理：在朴素集合论中，如果P是一个谓词（Predicate），那么\lbrace x| P(x)\rbrace是一个集合，这叫做集合的概括原则(Principle of Comprehension)¹(相信任何已经学过高一数学中集合相关内容的人都应该明白这个原则的含义)，该原则基本上描述了“满足某种特征的所有个体x”是一个集合，比如，令谓词P(x) 为 x是成年人，那么集合\lbrace x|P(x)\rbrace就是所有成年人的集合。
  概括原则在数学的层面上给了人描述“某一类个体”的能力，然而问题在于，在朴素集合论中，并没有对谓词P做任何限制，同时也没有区分集合与集合之间的区别，也可以同时包含个体(individuals)，也可以包含其他的集合。特别的，由于没有做任何限制，因此一个集合也可以包含他自身，于是，罗素在1901年在他写《数学原理》²的过程中发现了这个著名的悖论，其形式化描述如下：

令R=\lbrace X|X\notin X\rbrace，则有：

X\in X\to X\notin X

也就是说，如果令集合R是“所有不属于自身的集合所组成的集合”，则可以从“R是否包含其自身”推出悖论：

1. 集合R不包含自身，那么根据定义，R由所有不包含自身的集合所组成，因此R应该包含自身
2. 集合R包含自身，那么根据定义，R由所有不包含自身的集合所组成，因此R不应该包含自身

罗素悖论有多种不同的描述，其中最出名的是理发师悖论(Barber's Paradox)（也是由罗素本人提出的，用于更形象的描述这个悖论）

村里有一个只给不给自己理发的人理发的理发师，那么这个理发师该不该给自己理发？

稍加思索就可以从这句话里推导出和上面相同的结论，该悖论还有一个比较相似的陈述：说谎者悖论(Liar's Paradox)，这个悖论非常简单，只有一句话：

“这句话是假话”这句话是真话还是假话

值得一提的是，罗素悖论虽然对后世影响深远，但是在发现伊始，这个悖论并没有在数学界掀起什么太大的波澜，这种平静一直持续到1902年，罗素写给戈特洛布·弗雷格（Gottlob Frege）的一封信为止。

ia. 戈特洛布·弗雷格与Begriffsschrift（《概念文字》）

  1879年，戈特洛布·弗雷格(Gottlob Frege) 发表了著作 Begriffsschrift，中文一般译作《概念文字》，在这本书中，弗雷格表达了对以往使用自然语言描述数学的不满，他写到：

"... I found the inadequacy of language to be an obstacle; no matter how unwieldy the expressions I was ready to accept, I was less and less able, as the relations became more and more complex, to attain the precision that my purpose required."

-- Begriffsschrift； Gottlob Frege p.5

因此在这本书中，他首次提出了形式逻辑的概念并且在书中创建了一套形式逻辑系统，而后在他的另一本著作Grundgesetze der Arithmetik(中文一般译作《算术基础》)中，他使用自己创造的这套逻辑体系描述了一些基础的数学理论，这本书以及其中概念的出现是具有里程碑意义的³——但是我们在这里并不关心这些，我们只关心罗素在进行阅读后所认为的该书所描述的系统的漏洞，罗素在给弗雷格的信中描述了该悖论的构造方法：

定义f(x)=\neg x(x)，有：⁴

1. 如果f(f)，那么根据f的定义，有\neg f(f)
2. 如果\neg f(f)，那么根据f的定义，\neg f(f)=\neg\neg f(f)=f(f)

因此，从上面的定义中即可以得出f(f)，也可以得出\neg f(f)，也即推出了悖论

值得一提的是，弗雷格当时已经发现了并且重视到了函数与对象之间的区别：他规定函数必须需要接受对象作为参数，并且对象不能像函数一样被应用，也就是对于对象 x，x(x)是不合法的，因为只有函数才能被应用；并且函数本身也不是对象，也就是不能把函数本身作为参数传递给自身或者别的函数，例如f(f)或者f(g)。因此，弗雷格在回信中告诉罗素，类似f(f)这样的构造在他的系统中是不成立的，因此这个悖论也不成立。不过，几乎在反驳罗素的同时，弗雷格就沮丧地发现了另一个在自己的系统下推导出这个悖论的方法，更令他感到痛苦的是，这个悖论似乎直接摧毁了整个系统的基础——使得他的系统不再自洽。这要源于弗雷格对函数的像(Image)⁵的定义：

如果函数\Phi(x)与函数\Psi(x)在对于任何相同的参数都拥有相同的值，则说\Phi(x)与\Psi(x)具有相同的像(Image)，函数\Phi(x)的像用\hat{x}\Phi(x)表示(其中x可以被换成任意字母)

上面这段定义可以形式化的描述为：

问题在于，函数的像在这套系统中被弗雷格当做对象来对待，也就是函数的像可以被作为参数传进别的函数里，然而像的概念本身在某种程度上又可以视为对函数的一种定义(他描述了函数所有的参数与对应参数的值)。因此，虽然诸如f(f)这种函数对函数的直接应用被排除了，类似的事情却可以借助于像的定义而重现，弗雷格在Grundgesetze的第二卷中给出了该悖论的详细推导过程，首先，定义函数f(x)为：

本段接下来的部分是在弗雷格系统中对该悖论的纯数学推导，看懂这一部分至少需要高中逻辑学知识（简而言之就是至少得能看懂逻辑符号），如果你对纯数学内容不感兴趣或者还没有学过高中相关内容可以跳过。

(注意\hat{\alpha}\varphi(\alpha)代表函数\varphi(\alpha)的像)

这个函数很难理解？没关系，不要去尝试理解，他的唯一目的是构造一个悖论出来，因此本身可能没有任何意义。接着，令K为f(\sigma)的像，也即K=\hat{\sigma}f(\sigma)，由(1.1)我们可以得出，对任何函数g(x)：

(这一步是对(1.1)的直接应用，用K来实例化(1.1)中对a的量化)

而这进一步蕴含了对于任何函数g(x)：

(这一步可能有点难理解，(1.4)的意思是，假设有f(K)，则如果函数g的像等于K(也即\hat{\sigma}g(\sigma)=K)，则有g(K)。因为K是f的像，函数g的像等于K就相当于函数g与f同像，因此对于相同的参数K，f(K)与g(K)的值也相同。)

又因为(1.4)可以应用在任意函数g(x)上，我们可以加一个全称量化：

(这一步和(1.4)相比除了给g加了一个全称量化并且重命名成了\varphi以外没有任何变化，引入全称量化的原因是很显然的，而重命名更是什么都不影响，你在编程语言里改下函数参数的名字会影响这个函数的逻辑吗？不会。)

另一方面，假设我们有\forall \varphi.((\hat{\sigma}\varphi(\sigma)=K)\to \varphi(K))，则可以用任何一个函数h(x)去实例化\varphi，特别的，如果我们用函数f去实例化，则有：

(这一步里\to的前件是一个假设！不要问\to左侧是从哪里来的，他是个假设！假设是可以凭空出现的！)

然而巧合的是，K的定义恰好是f的像，也就是\hat{\sigma}f(\sigma)，因此\hat{\sigma}f(\sigma)=K成立，所以：

(这一步就是把已经知道一定成立的\hat{\sigma}f(\sigma)=K从(1.6)中移除后得到的，其余部分不变)

用f的实际定义(1.2)替换f(K)，可以得到

(这一步就是用f的实际定义替换了箭头右侧的f(K)，并且把实际定义中的形式参数x换成了实际参数K，其余部分保持不变)

注意\to两侧除了一个\neg符号以外完全一致，因此，我们获得了一个形如p\to \neg p的公式，通过归谬法⁶，我们可以推断出：

也即f(K)(是不是快忘了f(K)的定义了，快回头看一眼)

现在，既然我们推出了f(K)，就可以回过头来应用(1.5)，得到

也即\neg f(K)，也就是说，我们同时推出了(1.9)和(1.10)两个截然相反的结果。

弗雷格之所以会感觉这个悖论是灾难性的，是因为有一条被称作ex falso quodlibet的推理规则，这条规则意为，如果你能推导出一个悖论，那么可以从这个悖论出发推导出任何语句（因此这条规则又被形象的成为爆炸原则（Principle of Explosion）：如果你能推出悖论，那么一切都乱了套了，所有命题都会和爆炸一样跟在这个悖论的后面成立），也就是，对于所有的语句（命题）\varphi，有⁷：

\bot\vdash \varphi

这意味着，如果一个系统是不自洽的（可以推导出悖论），那么该系统中的所有命题，无论荒唐与否，都可以被证明是成立的，这就直接让这个形式系统失去了它存在的意义。

ib. 罗素与“恶性循环原则(Vicious Circle Principle)”

  不难看出，弗雷格系统的悖论的核心是设法通过将能够代表函数的像传递给其代表的函数自身作为参数，这与罗素在康托尔的朴素集合论中发现的悖论有着异曲同工之妙，在这两个悖论里，都出现了“对象的定义中包含了该对象自身”这样一个循环，或者叫自我指涉(Self-Referencing)，罗素发现了这些悖论的相同之处，在他的鸿篇巨著Principia Mathematica中(顺带一提，本书的名字是拉丁语，其中Principia的发音是Prin-/ki/-pia或者Prin-/t͡ʃi/-pia，而不是Prin-/si/-pia)，罗素提到：

[...] The vicious circles in question arise from supposing that a collection of objects may contain members which can only be defined by means of the collection as a whole. Thus, for example, the collection of propositions will be suppose to contain a proposition stating that "all propositions are either true or false", It would seem, however, that such a statement could not be legitmate unless "all propositions" referred to some already definite collection, which it cannot do if new propositions are created by statements about "all propositions"

--Principia Mathematica; Bertrand Russell p.37

罗素认为，之所以会出现这样的悖论，是因为类似的悖论通过在所有对象上的属性p来定义一个对象，而因为这样定义引入了所有对象，那么这个定义本身所定义的新对象也应当属于这个所有对象的范畴，因此也应该满足定义中的在所有对象上的属性p，而这就导致了一个定义上的循环，通过精心选择属性p的定义(例如在朴素集合论的悖论中令p为X\notin X)，就可以构造出悖论。而避免这种悖论的方法，就是要求如果某个对象的定义中涉及了所有对象，那么被定义的这个对象与其定义中涉及的所有对象不应当属于同一类别，也就是说，如果一个对象的定义涉及了所有的集合，那么这个对象本身一定不是一个集合。如果用“所有不属于自身的集合”来定义R，那么这个定义就涉及到了“所有的集合”，因此R一定不能是一个集合。

你可能会好奇，从“所有不属于自身的集合”这个描述来看，似乎并不代表“所有的集合”，而仅仅是全体集合中“不属于自身”的那一部分，为什么这里也认为这个定义涉及了“所有的集合”呢？这实际上是由于自然语言的歧义导致的问题，命题“所有不属于自身的集合”的形式化描述是：

\exists Y.\forall X.(X\in Y\leftrightarrow X\notin X)

这个公式中包含一个量化符号\forall，而其量化的对象包含所有集合X，因此，尽管该定义的结果是“全体集合中的一部分”，但是这“一部分”却是通过在“全体集合”上面的量化得到的，因此依然落入罗素所言的范畴。

罗素将这个规定称为恶性循环原则(Vicious Circle Principle)：

[...]: "Whatever involves all of a collection must not be one of the collection"; or, conversely: "If, provided a certain collection had a total, it would have members only definable in terms of that total, then the said collection has no total."

--Principia Mathematica; Bertrand Russell p.37

ii. 解决悖论的几种方案

  弗雷格最初提出他的形式系统的设想是让所有的数学理论都可以使用该系统的语言被描述，虽然他作为一个先驱者理所当然的失败了，并且在诸多教材和论文中总是被当做罗素悖论的第一个受害者对待，但是他的尝试、在Begriffsschrift与Grundgesetze der Arithmetik中提出的理论却为数学开辟了一片新的领域，这种对组成数学的基础，包括对数学理论本身的描述的研究，现在被称为数学基础(Foundations of Mathematics)，对数学基础的研究（很大程度上由于罗素等人的“数学=逻辑”这一命题）催生了数理逻辑(Mathematical Logic)，而弗雷格书中提出的用于描述数学理论的理论成为了现在的一阶逻辑(First-order Logic)。在上一节中提到，罗素在Principia Mathematica中总结出了恶性循环原则用以避免悖论，然而，罗素当时的描述是相当非正式的，在罗素提出的恶性循环原则基础上，其他数学家们提出了多个可以用于避免悖论的形式系统，除此之外，也有一部分人选择通过改变对数学本身的认知而避免悖论。

iia. 公理化集合论

  公理化集合论恐怕是对罗素悖论最为出名的解决方案，在罗素悖论，布拉利-福尔蒂悖论（Burali-Forti Paradox），与康托尔悖论（Cantor's Paradox）⁸等基于自我指涉的悖论被提出后，恩斯特·策梅洛（Ernst Zermelo）发现之所以会出现这类悖论，是因为朴素集合论的概括原则没有附加任何限制。“如果能够想办法避免x\notin x这种会引起自我指涉悖论的谓词在集合的构造中出现的话，就可以避免这类悖论了”，基于这一想法，策梅洛与亚伯拉罕·弗兰克尔（Abraham Fraenkel）提出了策梅洛-弗兰克尔集合论（Zermelo-Fraenkel Set Theory），简称ZF集合论。与朴素集合论的非形式化定义不同的是，ZF集合论是公理化（Axiomatic）的，公理化方法是一种“严谨的”方法，这意味着它采用一套严格遵循特定语法和规则的符号系统来代替自然语言表示命题和定理，并且使得该系统内的定理和性质可以从最初定义的几条公理出发，根据逻辑框架内的推导规则（诸如常见的三段论就是一个典型的推导规则）进行形式化的推导和证明，而不是像朴素集合论那样使用一套自然语言描述的系统，其证明和推导也同样是“不严谨的”。ZF集合论拥有着使用一阶逻辑来描述的数条公理(这也是为什么ZF集合论被称为是一阶理论（First-order Theory） )。其中的一条公理——概括公理（Axiom of Comprehension），就对应着朴素集合论中用于描述集合构成的概括原则：如果我们定义\vec{x_n}\equiv x_1,...,x_n，那么给定n元谓词P(\vec{x_n})⁹，有：

这条公理意味着，构建集合A的时候，A中的元素不仅要满足谓词P(\vec{x_n})，同时还必须已经是任意某集合B的元素。通过这种方式从公理上杜绝了罗素悖论：如果我们要用\lbrace x|x\notin x\rbrace来构造一个集合R，那么该集合中的元素x不仅要满足不是自身的元素这一点，还需要已经是另外的某个集合B的元素，换言之，R必须是某个集合B的子集——然而我们并不能构造或者证明这样的一个B存在，因此也就无法构造出R。
  值得一提的是，除了概括公理以外，ZF集合论还包含一条正则公理（Axiom of Regularity）：

这条公理乍一看比较迷惑，没关系，我们可以换一种方式来理解；假设X_0是一个嵌套的集合（也就是集合的集合），则有某个集合X_1是X_0的一个元素，而X_1本身也可能是一个嵌套的集合，同样的也会有集合X_2\in X_1，这样一直下去可以构造出一个由\in构成的“链条”：

正则公理指出这个链条不可能是无限长的，最终这个由\in构成的链条会停在某个不是嵌套集合（或者是个空集）的集合X_m处，也就是说，一个集合的嵌套深度不可能是无限的。这个规则使得ZF集合论拒绝了“包含自身的集合”这种构造，因为如果一个集合X包含自身，也即X\in X，那么就可以很轻易的构造出一个无限长的\in-链条出来：

而这与正则公理是相违背的。
  除了作为罗素悖论的一个解决方案以外，ZF集合论同时还是一个被广泛应用为数学基础的系统，ZF集合论已经被作为基础在其之上公理化了大量现有的数学理论。与ZF集合论同时作为罗素悖论的解决方案出现的其他公理化集合论还有Willard Quine的New Foundation，以及冯·诺依曼和哥德尔等人的Von Neumann–Bernays–Gödel集合论等，这些集合论各有优劣，分别都发展出了一套属于自己的理论体系。

iib. 数学哲学

传统数学与形式主义的观点对冲

  曾经的数学研究者们对数学持有柏拉图式的观点：数学是一个宏大的宇宙，其中包含了各种各样本来就已经客观存在的数学对象，而构造集合的本质是从这些已经存在的对象中挑选一批符合条件的出来，比如\lbrace x\in\R|x<2\rbrace就是从这些对象中，挑选出那些满足“小于2的实数”的对象出来。一直以来，数学这个学科都被理解为对现实世界法则的形而上的抽象，康托尔本人就把集合当做对“一组物品”的抽象，在康托尔的眼里，任何能被描述出来的一组物品都可以称为一个集合。因此朴素集合论中也从来没有思考过“形式化”的定义一个集合。这种传统的观念在19世纪末随着罗素悖论的发现遭到了沉重的打击，这使得人们开始思考这一问题是否可以通过“改变对数学的根本看法”来解决。
  以希尔伯特与弗雷格为代表的形式主义就在这个过程中产生了，他们认为，罗素悖论之所以能出现，是因为以往看待数学的这种形而上的视角，让数学变得“不严谨”：这种让数学和物理世界联系的认知限制并且迷惑了对数学的看法，因为数学和现实世界有诸多矛盾之处。既不应该像康托尔那样用自然语言来“挑选”对象，也不应该用自然语言来陈述事实。正相反，数学应当采用一种相当符号化的观点：也即，数学应该是由符号、文法和推导规则构成的，其理论和公式可以用符号串来描述（比如上文中的几条公理就是这样的符号串），而符号在串中的排布和顺序是根据文法决定的；除此之外，一组推导规则会指定如何从一个满足特定形式的符号串转换成另一个符号串；而数学证明，则是从一组符号串出发，根据推导规则尝试最终变换成目标的符号串。当然，这会引入一个新的问题：当我们去阅读这些符号的时候，它们代表什么，仅仅就是本身不包含任何意思的符号而已吗？虽然形式主义摒弃形而上的观点，但是总还是要提供一种方案来“解释”这些符号。于是，形式主义者们保留了柏拉图式的数学中，数学对象是客观存在的这一形而上的观点，也保留了“从这些对象中选取一部分出来”这种方式，只不过“选取对象”的方法从不严谨的自然语言，变成了严谨的由符号组成的公式。一个简单的例子就是，如果想要从所有这些客观存在的对象中选出“小于2的实数”，从传统的角度来看，“小于2的实数”这句话本身就够了；而形式主义者眼中，则应该用\exists Y.\forall x.(x\in Y\leftrightarrow x\in \R\land x<2)来精确的表达。而面对罗素悖论，形式主义者们举起了公理化这面大旗，通过对形式化之后的系统的公理做修改，来杜绝自指集合的构造（详见iia.）。

  如果你曾经学过形式逻辑，那么对上面这段描述应该相当熟悉，以一阶逻辑为例，符号就是一阶语言的字母表以及逻辑联结符；文法就是一阶逻辑对公式（Formula）的定义（也就是“长什么样的符号串算是一个一阶逻辑的公式”）；而推理规则则是各种各样的演绎系统（Natural Deduction，Hilber System，Sequent Calculi，Tableaux等等不一而足）；至于最后对符号的解释，则对应结构（Structure）与模型（Model）的概念。
  事实上，这种形式化方法的应用相当广泛，即便你没有学过形式逻辑，那么在计算机科学中也应当略有耳闻。例如在编译原理中，符号对应的是分词器（Tokenizer）的Token，文法对应的是编程语言的语法（Grammar）（一般是上下文无关文法（Context-free Grammar）描述的），而证明则对应编译器的解析（Parsing），也就是针对特定字符串，确定该字符串是通过哪些语法规则被生成的。

直觉主义

  在对悖论的研究中，除了有传统数学和形式主义的对冲，还诞生了一种新的思想：由鲁伊兹·布劳威尔（L.E.J. Brouwer）等人创立的直觉主义。在直觉主义者眼里，数学不应当是在纸上对干巴巴的符号进行操作，而是有实指的，数学描述了各种各样的对象，并且和这些对象是紧密相连的。克劳威尔认为，时间是唯一先验的概念，对数学的理解和知识则源于对时间的感知，而类似自然数则是随着时间的流动产生的¹⁰：

This intuition of two-oneness, the basal intuition of mathematics, creates not only the numbers one and two, but also all finite ordinal numbers, inasmuch as one of the elements of the two-oneness may be thought of as a new two-oneness, which process may be repeated indefinitely; this gives rise still further to the smallest infinite ordinal number ω. Finally this basal intuition of mathematics, in which the connected and the separate, the continuous and the discreet are united, gives rise immediately to the intuition of the linear continuum, i.e., of the “between,” which is not exhaustible by the interposition of new units and therefore can never be thought of as a mere collection of units.
--Intuitionism and Formalism; L.E.J Brouwer

而集合的构造也是采用这样的方式，对于形式主义者来说，无限集合不过是一个先验的、客观存在的概念，而对于直觉主义者来说，不存在真正的无限，如果要构造一个无限集合，相比起描述这个集合中元素满足的特性，直觉主义者要一步一步的“生成”这个集合中的所有元素，在任何一个特定的时间点，一个“无限集合”实际上都只包含到这个时间点为止生成的所有有限个元素，只不过这个“生成”的过程可以无限持续下去¹¹，因此，在直觉主义者看来，“无限”并不是一个先验的定义，而更像是一个有始无终的程序。也正是因为直觉主义对集合的“构造性”的要求，布劳威尔拒绝了不可数无穷大的集合（例如实数集R），而是转而用别的方法定义这样的集合中的元素（布劳威尔使用了一种他称其为Choice Sequence的方法定义实数）。
  上面提到，对于直觉主义者来说，集合并不是先验的，而是需要一步步构造出来的，不仅如此，直觉主义实际上采用了与传统数学和形式主义分别对立的两种观点：

1. 数学的宇宙中什么都没有，任何对象都需要手动“构造”出来
2. 数学并不仅仅是本身不自带任何意义的符号串，实际上，数学与其构造出的对象们是紧密相关的

其中第二点蕴含了直觉主义的另一个和形式主义完全相对的观点：由于数学纯粹是人类思维（通过对时间的感知而来）的产物，因此其核心是“构造”的过程，而不是“描述”的方式。这一点在布劳威尔对集合的观点中也能得到印证，集合来源自其随着时间一步一步的构造，而不是形式主义者角度下对一类对象性质的描述——也即，数学与描述数学的方式之间没有任何联系，无论是用传统数学中的自然语言，还是用形式主义者笔下的形式系统，都只是对人类思维的一种记录方式，它们唯一的作用是告诉另一个人这段记号的作者在记录时的思维方式，以便阅读的人在自己的脑海中复刻这段思维过程——也就是说，记号的作用是方便人与人之间的交流，仅此而已。
  因此，罗素悖论在直觉主义中是无法成立的，在罗素悖论中，集合R和R中的元素同样都是客观的存在，R的构成直接由R的描述（X\notin X）决定，因此才能够有“R是否属于R”这种命题，而在直觉主义逻辑中，不存在对R的描述（或者说对R的描述不对其构成产生任何影响），有的只是像上文中提到那样的对R的逐步构造，而在每一步（任意一个时间点）的构造的过程中都是不可能引入R自身的。

为什么说“R的构成直接由R的描述（X\notin X）决定，因此才能够有“R是否属于R”这种命题”？因为应当被注意到的是，首先，柏拉图式的观点蕴含了R中的元素在R被构造之前已经是客观存在的，因此，对R的构造才能基于对性质的描述来完成（对性质的描述从所有数学对象中“筛选”出了那些满足该性质的。如果从直觉主义的观点来看，这种先验的数学对象是不存在的，就更不用说从其中筛选出具有特定性质的了）；而罗素悖论的两个情况R\in R和R\notin R的分析都是基于对R的描述“所有不属于自身的集合所构成的集合”这句话的，同时R的构造也基于这句描述。而直觉主义下，集合的构成是通过一个“程序”一步步的构造其内部的元素来决定的；因此罗素悖论中基于对R的描述而对悖论进行的分析不成立。

  直觉主义不仅影响了对数学的看法，也影响了相应的证明过程。与经典逻辑不同的是，在直觉主义逻辑中，一个命题是成立的，当且仅当这个命题是可证的（Provable）；无独有偶，如果要证明一个对象存在，那么必须给出一个构造该对象的方法。经典逻辑中的排中律（Law of Excluded Middle）与双重否定律（Law of Double Negation）在直觉主义逻辑中都不成立：排中律的描述A\lor\neg A假设了A和\neg A其中之一的证明是一定存在的，然而，直觉主义认为有些命题既无法证明也无法证否，而有些命题在当前这个时间点上还没有找到证明或者其否定的证明（例如哥德巴赫猜想或者孪生素数猜想），因此一个命题和其否定在直觉主义逻辑中可能都不成立；双重否定律的描述\neg\neg A直觉上意味着“不存在‘A没有证明’的证明”，然而这很明显要比“A的证明”这一命题要更弱。
  基于“真实性=证明”这一观点，直觉主义者们，准确来说，由阿兰德·海廷（Arend Heyting）与安德雷·尼古拉耶维奇·柯尔莫哥洛夫（Andrey Nikolaevich Kolmogorov）给出了直觉主义逻辑中对一系列复合命题的证明的构造方法，被称为布劳威尔-海廷-柯尔莫哥洛夫诠释（Brouwer-Heyting-Kolmogorov Interpretation），简称为BHK诠释，令\mathtt{Prf}(P)是对P的证明¹²，则BHK诠释是在复合命题结构上的归纳定义：

• 对P\land Q的证明是一个有序对\langle\mathtt{Prf}(P), \mathtt{Prf}(Q)\rangle
• 对P\lor Q的证明是有序对\langle 0, \mathtt{Prf}(P)\rangle或\langle 1, \mathtt{Prf}(Q)\rangle
• 对P\to Q的证明是一个函数f:\mathtt{Prf}(P)\to\mathtt{Prf}(Q)，它将一个对P的证明转换为一个对Q的证明
• 对\exists s\in S.P的证明是一个有序对\langle s, \mathtt{Prf}(P)\rangle
• 对\forall s\in S.P的证明是一个函数f:S\to\mathtt{Prf}(P)，他将一个S的元素s转换为对P的证明

你可能会注意到虽然BHK诠释中写了布劳威尔的名字，但是我却只说了其中两个人，因为布劳威尔在BHK诠释中的署名基本是名誉性质的：他本人实际上相当反对对直觉主义的形式化研究

iic. 类型论

  在讲Begriffsschrift那一节的时候就已经提到过，弗雷格在当时已经注意到了函数和个体的区别，他要求函数的参数必须是个体，而个体则不能像函数那样被应用。也就是说，如果f是一个函数而x是一个个体，那么f(f)和x(x)都是不合法的，这也使他的系统避免了罗素对悖论的第一种描述，然而，这最终并没能避免这种悖论的发生。罗素在此基础上进一步总结出了恶性循环原则，并且提出了属于自己的解决方案：分支类型论（Ramified Theory of Types）。
  在恶性循环原则中，罗素要求如果如果一个对象的定义量化了全体的集合，则这个被定义的对象一定不是一个集合。罗素悖论并不是唯一符合这样一个定义的概念，罗素指出，有些定义并不涉及“全部”“所有”等量化，例如在罗素给出的一个例子中：

拿破仑是科西嘉人

就不包含任何量化，类似“是科西嘉人”这样的定义/谓词被罗素称为是直谓的（Predicative），而

拿破仑拥有所有好将军应当拥有的特质

包含了对“所有将军”的量化，这样的定义被认为是非直谓的（Impredicative）。有许多非直谓的定义都可能带来危险性，例如“数字是所有满足数字上面的归纳属性的对象”，这是一个非直谓的定义，然而很容易就能证明其本身也是一个归纳属性，这样就又陷入了恶性循环中。
  分支类型论，听起来像是类型论的某个分支，但是其实该理论是最初的类型论，在Principia Mathematica中，罗素第一次提出了类型（Type）的概念。相比起弗雷格，罗素认为不仅函数和个体之间存在区别，函数与函数之间也存在区别，有接受函数作为参数的函数，也有接受个体作为参数的函数。在恶性循环原则中，罗素要求如果如果一个对象的定义量化了全体的集合，则这个被定义的集合一定不是一个集合。在Principia Mathematica中，罗素更加详细的贯彻了这个观点，他提出不仅数学对象拥有类型，类型同时也拥有自己的阶（Order），罗素称之为分支层级（Ramified Hierarchy），简言之，如果一个对象的定义量化了全体处在第n阶的对象，那么这个对象本身处在第n+1阶，而第n+1阶的类型与第n阶的类型是不同的，因此这样被定义的对象一定不属于其定义中量化的全体n阶对象的范畴。因此，如果有一组数字处在n阶，那么由“满足这些数字上面的所有归纳属性”所定义的数字处在n+1阶，自然不可能和n阶的混在一起。
  实际上，还有一个与分支层级不谋而合的概念，阿尔弗雷德·塔斯基（Alfred Tarski）面对说谎者悖论时，提出了元语言（Metalanguage）和目标语言（Object-language）的概念，塔斯基认为，面对“这句话是错的”这种定义时，要分清定义本身和被定义的对象，被定义的对象所处的等级要比定义本身更低，而我们可以通过要求高等级的语句只能从低等级的语句组成的定义得来来避免说谎者悖论：“这句话是错的”本身定义了一个比这句话本身层级更高的概念，因此其定义的对象不被计入这句话所描述的范围内。
  这种通过给不同定义下的对象“分层”的方法似乎看起来一劳永逸的解决了悖论，但是引入了一个新的问题，那就是并非所有非直谓的定义/属性都会带来问题，事实上，有相当多的现有定理的描述都是非直谓的。而分支类型论的限制性实在是太强了，不同层级之间的对象被完全分隔让这些定理的证明变得相当繁琐甚至彻底失效。罗素在提出分支类型论的同时就意识到了这一点，因此他也在同时提出了可归化公理（Axiom of Reducibility），其内容大致为处在任何阶的定义/谓词，都会有一个在一阶的定义/谓词与之等价。这导致了一个很严重的问题，那就是该公理似乎让整个分支层级失去了意义，他代表着任何阶的定义都可以被归约到一阶。事实也的确如此，不久之后，弗兰克·拉姆齐（Frank P. Ramsey）与阿隆佐·邱奇（Alonzo Church）等人发现，说谎者悖论由元语言和对象语言的混淆造成的非直谓性的定义本身无伤大雅：只要能够根据上下文分清楚哪些是元语言，哪些是对象语言就足够了，而分支层级正式为了避免这种语言性质的非直谓性定义才出现的。因此，邱奇等人从分支类型论中去掉了分支层级，而只留下来简单的函数与对象，以及不同参数的函数之间的类型区别。称之为简单类型（Simple Types），事后证明了简单类型已经足以避免悖论的产生。

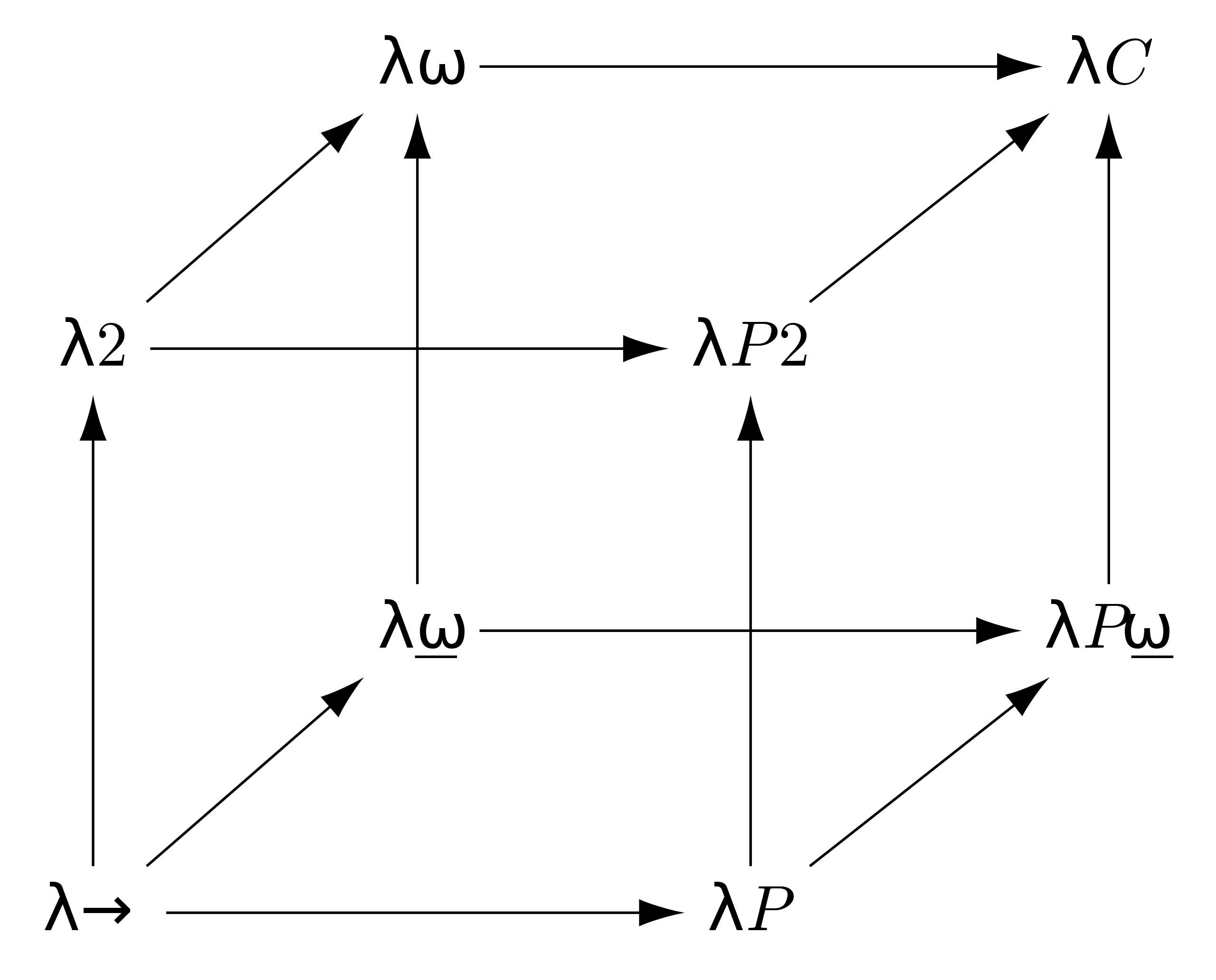
  经过一百余年的发展，类型论已经在数学和计算机科学中广泛地被应用。在数学中，类型论，尤其是佩尔·马丁-洛夫（Per Martin-Löf）基于直觉主义逻辑的直觉类型论（Intuitionistic Type Theory）被应用于数学基础相关的研究，并且在上面发展出其他分支，例如符拉基米尔·弗沃特斯基（Vladimir Voevodsky）的同伦类型论（Homotopy Type Theory）。而在计算机领域，类型论的实践应用则更加广泛，现如今，大部分的编程语言都包含了类型系统（Type System）用于静态检查，保证程序的语义和正确性，这些类型系统五花八门，有支持父子类型关系的子类型系统（Subtyping），有支持参数化类型多态的系统F（System F），有能够作为计算机辅助证明的类型系统构造演算（Calculus of Construction）。这些类型系统无一例外都发源自邱奇在\lambda-演算上定义的简单类型，而后者则源自对罗素的分支类型论的简化。

iid. 维特根斯坦的观点

  除开数学意义上各种解决悖论的方案以外，路德维基·维特根斯坦（Ludwig Wittgenstein）也提出了自己在哲学与语言角度的观点，维特根斯坦将符号（Symbol）与记号（Sign/Notation）当做两个不同的概念来对待，其中符号对应语义（Semantic），记号对应语法（Syntax）。记号是一个符号可以被人观察到的部分，不包含任何额外内涵，一个记号真正的含义（也就是它的语义，它对应的符号）是由使用它的使用方式决定的，例如\varphi就是一个记号，而这个记号所对应的符号真正的含义只有在它被使用的时候才能被确定，如果使用它的环境是\varphi(x)，其中x是一个个体，那么\varphi就是一个接受个体作为参数的函数；如果使用它的环境是\varphi(\sigma)，其中\sigma是一个函数，那么\varphi在这里的含义就是接受一个函数作为参数的函数。也就是说，同一个记号完全可以对应两个符号，这是由这个记号被使用的上下文决定的。以上观点可以在维特根斯坦的著作Tractatus Logico-Philosophicus，中译《逻辑哲学论》（以下简称Tractatus）中的以下几条里得到印证：

3.32 记号是一个符号中可以被感官感知到的东西。
3.321 故同一个记号（书写记号或声音记号等等）可以为两个不同的符号所共有——这时两者是以不同的方式在标示。
3.322 如果我们应用同一个记号，而以不同的标示方式来标示两个不同的对象，这样做决不能指示这两者有一个共同的特征。当然，这是因为这记号是未加规定的。因此我们可以选用两个不同的记号，这样，标示者一方还保持有什么共同点呢？
[...]
3.326 为了通过其记号来辨识一个符号，我们必须在有意义的使用中观察它。

--Tractatus; Ludwig Wittgenstein

接着，他提到了自己对罗素的类型论的批评，他认为，罗素在对类型论的定义过程中混淆了语法与语义的概念：罗素在定义类型论的过程中使用了诸如“类型”，“命题函数”这些词，而这预设了这些词是已经被定义了的，可是实际上这些词正是出现在对他们的定义中。在维特根斯坦看来，定义语法（记号）的时候，不应当涉及任何与该记号的语义（符号）相关的内容，而罗素对类型论的定义违反了这一点：他在对类型论的定义（对记号的定义）的过程中，使用了他正在定义的对象的语义（在定义中使用“类型论”等正在被定义的概念）：

3.33 在逻辑句法中，记号的指谓决不应该起任何作用。逻辑句法应该无须提到记号的指谓而建立起来；它仅仅以表达式的描述为前提。
3.331 根据这一见解我们回过头来看罗素的“类型论”：罗素的错误显然在于，他在建立记号的规则时必须提到记号的指谓。¹³
3.332 没有一个命题能够作出关于自身的陈述，因为一个命题记号不能包含于它自身之中（这就是全部的“类型论”）。

--Tractatus; Ludwig Wittgenstein

在确立了这些观点后，维特根斯坦紧接着提出了他对于罗素悖论的看法，他认为如果分清了语法和语义（记号和符号）的概念之后，罗素悖论就不攻自破了，在这里，他使用了类似罗素在给弗雷格的信中对悖论的描述：F(F(fx))，并声称其内部的F与外部的F含义不同：

3.333 让我们假设函项F(fx)可以成为它自身的主目，这时就会有一个命题F(F(fx))，其中外函项F和内函项F必定有不同的指谓，因为内函项具有\varphi(fx)的形式，而外函项则具有\psi(\varphi(fx))的形式。只有字母“F”对于两个函项是共同的，但是字母本身不标示任何东西。如果我们把F(F(u))写作“(\exists\varphi): F(\varphi u).\varphi u=Fu”¹⁴，这一点就立刻清楚了。这样罗素的悖论就消解了。¹⁵

--Tractatus; Ludwig Wittgenstein

维特根斯坦强调记号（语法）的意义（语义）这个记号被使用的环境，其中外部的F与内部的F在被使用的方法上来看完全不同，因此这两个F一定不是同一个东西，他们唯一的共同点是其记号都是F，然而就如同维特根斯坦在3.32到3.326中提到的那样，记号本身不能说明任何问题。
  除开在语言层面上对于罗素悖论的解释以及在对语义语法混淆上对罗素的批判，维特根斯坦对于类型论的意见还不止于此。在分支类型论中，每一个层级对数字和函数的定义都是不一样的，就像之前提到过的，第n阶的数组与第n+1阶的数字是不一样的，后者通过量化对第n阶数字的量化实现；同理，第n阶的函数与第n+1阶的函数也是不一样。而罗素对这些处在无穷无尽层级的不同对象，统一使用“数字”和“函数”来描述。在维特根斯坦看来，这不仅引入了“数字”和“函数”这两个定义上的二义性，而且还引入了一个更严重的问题，那就是对类型论的定义是不完备的，由于在每一个层级都需要重新定义这些概念，而层级又是无穷无尽的，因此，这些概念永远也没有办法被全部定义完成，维特根斯坦在此处引用了弗雷格的观点：

A definition of a concept (of a possible predicate) must be complete; it must unambiguously determine, as regards any object, whether or not it falls under the concept (whether or not the predicate is truly assertible of it)

--Gottlob Frege

由于这种定义的不完备性，维特根斯坦认为诸如“类型”，“函数”等概念的使用在这样的体系下是不明确的，因此，他拒绝认同罗素的分支类型论。
  你可能会注意到，维特根斯坦认为罗素混淆了语法与语义的一大原因是罗素在定义“类型”的过程中用到了“类型”这个词，因此产生了循环定义。这种问题是可以被解决的，邱奇在他后来对简单类型的形式化过程中，就通过形式化方法避免了这个问题，同时，邱奇还针对维特根斯坦在语义和语法上的观点发表了自己的看法：

Of course the matter of interpretation is in any case irrelevant to the abstract construction of the theory

--Alonzo Church

邱奇认为，理论本身是抽象的，其本身对应对象语言，而定义理论的文字则是元语言，对定义理论的元语言的任何解释都不应当影响到理论本身。元语言中存在的不明确性不会影响理论本身的精确性——它们要描述的意思很清楚。那么,这样的方法能够使得维特根斯坦认同类型论吗？并没有。原因是邱奇在规范简单类型的时候，依然规定了一些语法（记号）层面的概念的规则，比如对合式公式（Well-formed Formula）的定义。而维特根斯坦依然坚持认为记号的意义应当在其使用中被显现，而不是对记号本身给出定义/规则，他认为这些这个对记号的规则本身等价于符号（语义），因此其意义也被反映在符号之中：

5.514 一个记号系统一旦建立起来，其中就有一条用以构造一切否定p的命题的规则，一条用以构造一切肯定命题p的规则，一条用以构造一切肯定p或q的命题的规则，等等。这些规则等价于一些符号，它们的意义就反映在符号之中。

--Tractatus; Ludwig Wittgenstein

  维特根斯坦的观点，虽然没有收到数学界的广泛响应和认可，但是他和他的Tractatus在哲学上的影响则相当深远，作为一本以晦涩难懂而闻名的哲学书籍，Tractatus中的观点与思想吸引了相当多哲学家去探究不同角度的诠释。笔者对西方哲学史不甚了解，因此在这里对维特根斯坦在哲学领域的贡献不再多讲。

参考文献

1. (1995, December 8). Russell’s Paradox. Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/russell-paradox/
2. (2011, January 12). Formalism in the Philosophy of Mathematics. Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/formalism-mathematics/
3. (2009, July 18). Platonism in the Philosophy of Mathematics. Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/platonism-mathematics/
4. (2008, September 4). Intuitionism in the Philosophy of Mathematics. Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/intuitionism/
5. (2008, July 10). The Development of Intuitionistic Logic. Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/intuitionistic-logic-development/
6. (2006, February 8). Type Theory. Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/entries/type-theory/
7. Russell, B., & Whitehead, A. (1910). Principia Mathematica (2nd ed.). Cambridge University Press.
8. Russell, B. (1903). The Principles of Mathematics (2nd ed.). Cambridge University Press.
9. Wittgenstein, L. (1903). Tractatus Logico-Philosophicus (2nd ed., pp. 18-19, 60). Routledge.
10. Epstein, R. L., & Carnielli, W. A. (2008). Computability: Computable functions, logic, foundations of mathematics (3rd ed.). Advanced Reasoning Forum.
11. Kamareddine, F., Laan, T., & Nederpelt, R. (2005). A Modern Perspective on Type Theory: From its Origins until Today. Springer.
12. Polytopos (2020, April 14). Mathematical Intuitionism and the Flow of Time. AI ALIGNMENT FORUM. https://www.alignmentforum.org/posts/eNnr4JwEDNux63oXm/mathematical-intuitionism-and-the-flow-of-time
13. Brouwer, L.E. Intuitionism and formalism. Bulletin of the American Mathematical Society, 20, 81-96.
14. Davant, J. B. (1975). Wittgenstein on Russell's Theory of Types. Notre Dame Journal of Formal Logic.
15. Sutrop, U. (2009). Wittgenstein's tractatus 3.333 and Russell's paradox. Trames-journal of The Humanities and Social Sciences - TRAMES-J HUMANIT SOC SCI. https://doi.org/10.3176/tr.2009.2.06
16. Dubinsky, E. Meaning and Formalism in Mathematics. International Journal of Computers for Mathematical Learning 5, 211–240 (2000). https://doi.org/10.1023/A:1009806206292