本文介绍 Petrank [2006] 论文中的适用于增量并发回收器的垃圾回收算法:"The Compressor",并且专注于介绍其中的第一部分,也即该算法是如何计算压缩之后对象在内存中的位置的。在开始本文以前,有必要介绍一下压缩的原理,也即 Sliding Compaction(滑动压缩),这意味着内存中的对象被向内存中的一端“滑过去”,想象一个稀疏的羽毛球筒:当你想要整理这个球筒中的“碎片空间”的时候,你能做的事情就是把里面的羽毛球一个接一个的“滑动”到最内侧,这样里面的碎片空间就被“挤出来”到了外侧。
传统的垃圾回收算法中,Mark-Sweep与Mark-Compact是两种相当常见的算法,其中前者的时间消耗非常低,仅仅需要遍历一次堆就可以完成标记,但问题在于由于对象不会移动,被回收的对象会在堆上造成严重的内存碎片问题,这一点可以以来优秀的内存分配算法实现(常见的有 Segregated-Fits 与 Buddy System,后者也即 Linux 内核使用的)。然而,这样的内存分配一般要求将内存块放进诸如树或链表的数据结构中,从而导致新的开销。而时间开销最小的内存回收算法自然是 Sequential Allocation —— 也即在一块连续的内存空间上直接将未分配空间指针向后移动来分配一块新的内存(称为 Bump Pointer),其时间代价为常量。不过,Sequential Allocated 的内存在垃圾回收之后必然会造成严重的内存碎片问题,这要求垃圾回收器拥有压缩内存的能力,以此来解决碎片问题。许多压缩回收算法要求遍历堆至少两次:第一次用于计算压缩之后对象的位置,第二次用于更新对象的引用。所以大部分的类似算法通常拥有较差的吞吐量(消耗在垃圾回收上的总时间占比过大)。不过,在 Petrank [2006] 中,作者提出了一种只需要遍历堆一遍就可以完成压缩的算法,并将其命名为 "The Compressor"。
在介绍该算法之前,需要稍微介绍一下该算法应用到的技术,首先,与许多垃圾回收器选择在对象头中预留表示对象在可达性分析中存活的标记位不同,该回收器选择将标记位存在外部的一张表中,这样的好处是,由于所有的标记都紧凑的放在一张表中,因此遍历所有活对象时的内存局部性相当优秀。其次,由于垃圾回收器通常都会进行内存对齐,也即对象被储存在2的特定倍数的地址,因此 The Compressor 选择将堆分为大小相同的块(堆本身仍然是连续内存,只是可以通过模每个块中理论上的字节数来计算当前地址所处的块)。同理,由于内存对齐的存在,上文中提到的标记表1不需要映射每个可能的字节,而只需要映射对应对齐大小的字节即可。
例如,如果对齐大小是8,则标记表中的每个元素都对应了一块大小为8的内存:第一个元素对应0-7,第二个元素对应8-15... 以此类推,标记表中的某元素为
true2则意味着“该元素对应的内存起始位置上有一个对象”。
同许多算法一样,该算法的第一步是计算压缩之后每个对象的新地址,其伪代码如下:
computeLocation(HeapStart, HeapEnd, MoveToRegion):
// HeapStart 和 HeapEnd 代表要扫描的堆的起始和结束地址
// MoveToRegion 指向对象将要被移动到的内存区域,一般来说是 HeapStart
offset <- []
loc <- MoveToRegion
block <- 0
for b <- 0..numBits(HeapStart, HeapEnd):
if b % BITS_PER_BLOCK = 0:
offset[block] <- loc
block <- block + 1
if isMarked(bitmap[b]):
loc <- loc + BYTES_PER_BIT
接下来大致解释一下该算法中的函数和常量:
numBits(start, end)计算从start开始到end(其中start和end应当对齐)结束的这段内存中一共包含多少个标记位,由于每个标记位对应一段长度为一个字长的内存,因此该函数的返回值一般是(end - start) / W,其中W是字长。BITS_PER_BLOCK是每个块中对应的标记位数量,假设每个块大小为256字节,而每个标记位对应大小为1字节的内存,则BITS_PER_BLOCK=256/1=256。也即一个内存块对应256个标记位。BYTES_PER_BIT是每个标记位占的字节长度,之前说过,一个标记位一般对应一个字长,假设一个字长为1字节,则此处BYTES_PER_BIT就是1字节。
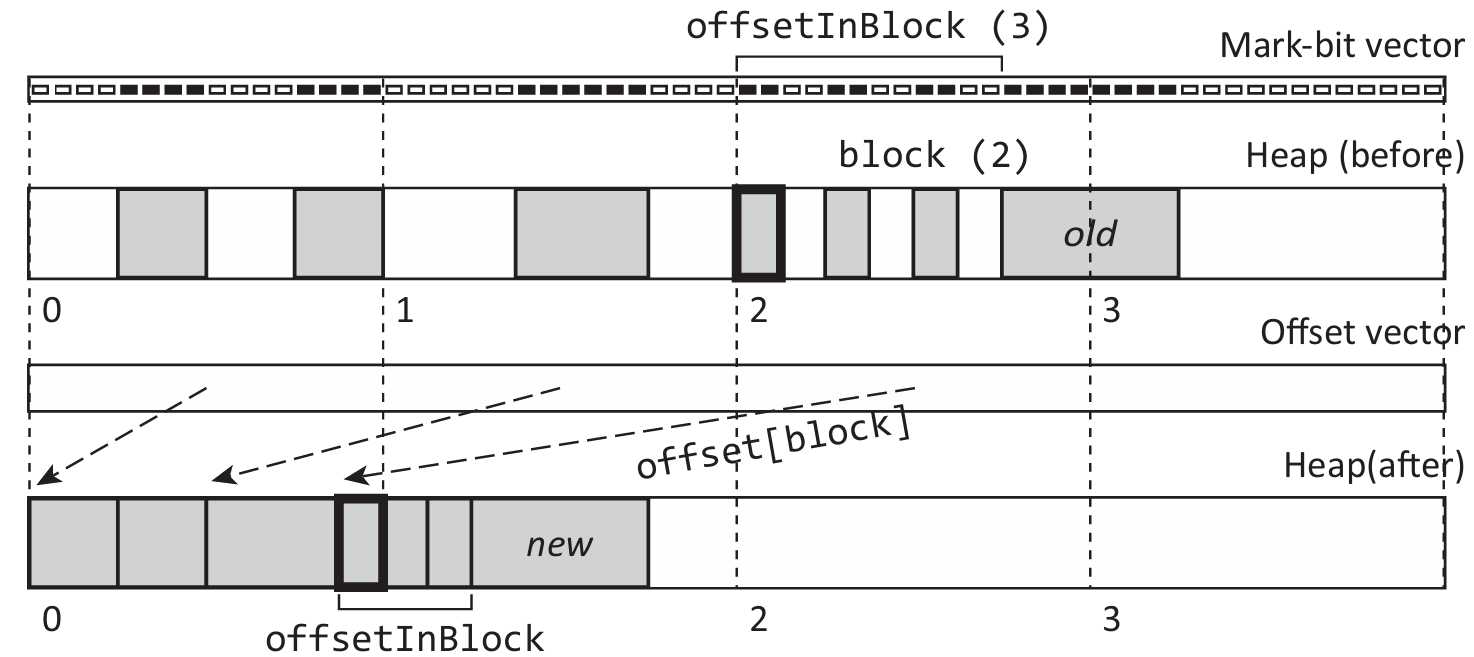
该算法的运行思路可以用这张图来解释:这张图的最上方是标记表,其中黑色的为true的标记,白色为false,任何堆上的活对象所对应的所有位都会被标记位黑色,第二行是在压缩之前的堆,第三行是计算得到的存有压缩后的每个对象的新内存位置的表,第四行则为压缩之后的堆。注意该算法从左到右遍历整个标记表,其中的 loc 字段表示了下一个扫描到的对象在压缩后可以被放在哪里。当他遇到 b % BITS_PER_BLOCK = 0,也即当前遍历的标记位进入了一个新的内存块时,就将 (block, loc) 加入到 offset 表中,这意味着 “新内存块中的下一个(也即第一个)对象可以被放到 loc 对应的位置”。接下来,算法判断标记表中的每一位是否被标记,如果是,则将 loc 指针向后移动一个标记位的大小,这一步的目的是将 loc 指针向后移动一个对象的大小,以图为例,假设一个标记位大小是1字节,注意第0个内存块中的第二个对象,当循环循环到这个对象的第一个字节时,这个字节对应的位是被标记的,因此 loc 会被向后移动,接着循环到第二字节时,其对应的第二位也是被标记的,因此 loc 再次向后推动一个字节,以此类推,一直到 loc 向后推动4个字节,也即
第二个对象的大小为止。
可以注意到,这个算法的核心是维护一个新的指针,同时算法遍历堆中的每个标记位,每当遇到一个新的活对象,就把指针向后移动这个对象大小的长度,由于只有在遇到活对象时指针才会被移动,因此这个指针所指向的这段压缩后的内存是紧致的,不会有内存碎片问题,不仅如此,每当遍历到一个新的内存块时,算法不仅会继续寻找活对象,还会标记这个内存块中的第一个活对象应该被放到的内存位置,这样,这个内存块中所有其他的活对象在压缩后内存中的位置都可以通过第一个活对象的内存位置计算得到,例如在上图的内存块2中,算法的offset表存储了该内存块中第一个活对象在压缩后的地址应当是第14标记位对应的地址,因此内存块2中的第2个对象的新地址就可以通过14 + size_of(first_obj)得到,也即第一个对象的起始地址加上第一个对象的大小。
依托构式的 Rust 实现
贴个 Rust 实现,这是我写的一个后端的内存管理器中的一部分:
// "The Compressor"
// Je voudrais référer à l'algorithme 3.4 et la figure 3.3 dans le livre.
pub unsafe fn compute_locations(&self, heap_block: &HeapBlock) -> HashMap<usize, *mut u8> {
let mut location = heap_block.start;
let mut block = self.block_index_of(heap_block.start, heap_block);
let mut offset = hashmap!{};
for (idx, bit_block) in self.bitmap[self.index_of_heap_block(heap_block)].iter().enumerate() {
for i in 0..8 { // 8: bits of byte
let bit_index= idx * 8 + i;
// il y a 256 bytes dans un bloc, et chaque bit répresente un mot qui a pour taille la taille d'un byte
// alors il y a en fait 256 bits per bloc.
// Pour examiner si le bit courant franchit le bloc, on vérifie si l'indice du bit est un multiple de 256.
// le code suivant répond à la question: "où devrait-on mettre le premier objet dans 'block'?"
if bit_index % BITS_IN_BLOCK == 0 {
// le premier objet dans 'block' sera mis à 'location'
offset.insert(block, location);
block += 1
}
if bit_set(*bit_block, i) {
let pointer = self.bitmap_index_to_address(BitmapIndex::new(self.index_of_heap_block(heap_block), idx, i));
location = location.byte_add((*pointer).size);
}
}
}
offset
}
注意到我计算numBits的方法稍有不同,因为我的实现里标记表是一个 Vec<u8> 数组,其中的每一物理位表示了一个标记位,因此标记表实际上是二维的,而在伪代码的算法中,标记表是一维的,现实中如果要做到一维的标记表,势必会浪费大量空间(一维标记表应该是Vec<bool>类型的,问题是一个 bool 本身会占据整整一个字节,其中有7位都是浪费的)。而如果想要不浪费空间,则必须使用位运算的技巧,这样标记表就必须是二维的Vec<u8>或者Vec<i32>。
接下来的一系列文章里可能会一个托管语言的内存管理器(或者直接说堆)的全部实现过程...大概吧。
封面
本文的封面图片来自@Misukitoko,是 BanG Dream! It's MyGO!!!!! 中的 要楽奈,猫猫可爱捏











Comments NOTHING