对KMP算法中前缀函数的分析以及正确性证明

[toc]

本文中用$P_n$表示$P[1..n]$，用$P[n]$表示$P$中的第$n$个字符，用$P_i\sqsupset P_q$代表$P_i$是$P_q$的后缀，用$P_i\sqsubset P_q$代表$P_i$是$P_q$的前缀，所有下标从1开始

因为太久不看完全忘记了KMP算法究竟是怎么实现的，看龙书的时候发现上面的题目赫然印着相关内容而我却完全看不懂，遂翻开算法导论大战一个多小时重温了这个各方面复杂度都十分优秀的字符串匹配算法   KMP算法是一种优化过的有限自动机匹配算法，和有限自动机需要花费$O(m|\Sigma|)$(其中$m$是模式串的长度)的时间生成状态转移表不同的是，KMP算法通过维护一张更小的表来尝试跳过不可能成功匹配的字符串并以此将”准备阶段”的效率提高的$O(m)$，在扫描阶段，KMP和有限自动机算法拥有相同的线性时间复杂度   KMP算法的核心基于这样的观察，假设匹配串$T=bacbababaabcbab$，模式串$P=ababaca$，当我们匹配到某一个位置的时候：

此时令$P$相对于$T$的偏移量为$s$，此例中$s=4$(本文中下标从1开始，遵循CLRS的规范)，已匹配长度为$q$，此例中$q=5$($ababa$)，在该情况下我们已经成功匹配了5个字符，但是第6个字符$a$和$c$不匹配，KMP的核心思想在于，当我们知道已匹配长度$q$和已匹配的字符串$P_q$，就能立即知道某些$s$一定是无效的，比如在这个例子中，$s+1$一定是无效的，因为当$s+1$时，我们有

$b$和$a$显然是不匹配的，但是，如果我们把$s$向右推进2，就变成了

此时$s’=s+1$，并且$P$和$T$中再次出现了长度$k=3$匹配，也就是我们通过把$s$推进2次跳过了五次多余的匹配，直接从$P[4]$开始，诸如类似$k$的值会被一个特殊的函数计算出来并储存在表$\pi$中，比如在上面的情况中就可以直接通过$\pi[q]=\pi[5]=3$来得到$k$的值并且把$s$推进$q-k=2$次，令$s’=s+(q-\pi[q])$，我们就可以在一次失败匹配后直接得到下一次匹配的开始下标。   很明显，我们的目的是跳过尽可能长的”无用”字符串，也就是不可能成功匹配的字符串，那么就存在一个这样的问题：

假设$P[1..q]$和$T[s+1..s+q]$匹配，找到一个最大的偏移量$s’$，使得对于$k\lt q$且$s’+k=s+q$，存在$P[1..k]=T[s’+1..s’+k]$ (这个描述比较拗口，但是可以结合前三张图示理解)

换言之，就是对在同一下标结束的匹配的字符串，比如上图中的两次匹配，一次$q=5$一次$q=3$，都在$T[9]$处结束，对于$T$来说，匹配的字符串的末端下标没有变化，我们已经知道$Pq\sqsupset T{s+q}$(不言而喻)，那么应当找出一个$k<q$，让$Pk\sqsupset T{s+q}$(这里的$s+q$可以换成$s’+k$，相当于下标$s$增加到了$s’$而匹配的文本串长度$p$长度减小到了$k$，在上面的例子中，下标$s=4$增加到了$s’=6$，而$q=5$减小到了$k=3$，两者互补最终的和依然是$9$)，既然我们的目的是增大”跳过”的数量也就是$s’$的值，我们又知道$s’+k=s+q$，在给定$s$和$q$的情况下，最大化$s’$值的方法自然是最小化$k$的值。而$k$的最小值自然是$0$，也就是对于任何$k\lt q$，都不存在$Pk\sqsupset T{s+q}$的情况

最佳情况演示 之前：

\def\a{\boldsymbol{a}} \def\b{\boldsymbol{b}} \def\c{\boldsymbol{c}} \begin{array}{ccccccccccccccc} b&a&c&b&a&b&\a&\b&\b&a&b&c&b&a&b& \\ &&&&&&\a&\b&\b&b&a&c&b \end{array}

之后：

\def\a{\boldsymbol{a}} \def\b{\boldsymbol{b}} \def\c{\boldsymbol{c}} \begin{array}{ccccccccccccccc} b&a&c&b&a&b&a&b&b&\a&\b&c&b&a&b& \\ &&&&&&&&&\a&\b&b&b&a&c&b \end{array}

$s$直接从$6$跳过了$q=3$变成了$s’=9$，这种情况下$k=0$，这种情况的前提是 根本不存在一个$k\lt q$使得$P_k\sqsupset T_{s+q}$，在上面的例子中，只有$abb$才是$abb$的后缀，往右挪动$P$，无论$ab$还是单$a$都不是$T_{s+q}$(或者$T_{s’+k}(k=0)$的后缀

此时我们需要做出另外一个观察，很明显，$Pq\sqsupset T{s+q}$，同时$Pk\sqsupset T{s+q}$并且$|P_k|\lt |P_q|$，这蕴含着$P_k\sqsupset P_q$，而根据上文中的图示可以看出同时$P_k\sqsubset P_q$。因此，我们的目标就是寻找一个最大的$k$使得$P_k$既是$P_q$的后缀又是$P_q$的前缀，总结出这一点，我们就可以填充表$\pi$了

令$\pi$是$\lbrace1,2,3,…,m\rbrace$到$\lbrace0,1,2,…,m-1\rbrace$的函数，有$\pi[q]=max\lbrace k\lt q且P_k\sqsupset P_q\rbrace$，换言之，就是要求$P_k$是最长的既是$P_q$前缀($k\lt q$本身就蕴含了$P_k\sqsubset P_q$)又是$P_q$真后缀的字符串，同时$P_k\neq P_q$，即$P_q$的 最长公共前后缀

我们先给出一个计算$\pi$的函数叫做前缀函数，接着分析该函数的正确性

该函数的核心思想基于这样的观察，考虑一个例子，如字符串$abab?$，假设我们已经知道了当前的最长公共前后缀是$ab$，也就是长度为2，那么当$?$是什么的时候，可以让该字符串的最公共前后缀长度为3？这个答案很明显是$c$，因为前三个字母$aba$是确定的，想要让公共前后缀长度为3，则前缀和后缀都必须是$aba$，因此只需要判断$a$是否等于$?$即可。现在设$P=ababaa$，要计算$P_0..P_q$中的所有子串的最长公共前后缀，首先设置两个指针$k$和$q$，其中令$k$的初始值是0，$q$是1，这代表第$q_0$不存在任何公共前后缀，接下来，我们尝试着模拟迭代，第一次迭代之前，$k=0$，$q=1$，令$\pi[1]=k=0$，代表第一个字符本身没有任何公共前后缀(因为我们要求后缀必须是真后缀，而单个字符的后缀只有它本身，不满足真后缀要求)，我们有

指针指出了$k$和$q$现在的位置，接着我们进入第一次迭代，此时$k=0$，$q=2$，我们比较$P[k+1] $和$P[2]$是否相等，很显然$a\neq b$，因此我们让$\pi[q]=\pi[2]=k=0$，也就是$P_2$不存在任何公共前后缀，此时进入第二次迭代，进入第二次迭代前有

此时再次比较，发现$P[k+1]=P[q]$，此时将$k$递增1，令$\pi[q]=\pi[3]=k=1$，代表$P_q=P_3$有长度为1的最长公共前后缀，代表进入第三次迭代，进入第三次迭代前有

依然符合$P[k+1]=P[q]$，于是$k$再次递增1，$\pi[q]=\pi[4]=k=2$，继续下去有

依然$P[k+1]=P[q]$，递增$k$，$\pi[q]=\pi[5]=k=3$

好，现在我们发现了一个问题，$P[k+1]\neq P[q]$了，但是$k=3$，这时候我们该怎么填$\pi[6]$呢，简单的直接把$k$归零肯定是不行的，因为很明显上图中$\pi[6]$应当等于$1$，解决办法是这样的：我们把$k$从当前的位置开始往后倒着推，找出之前的每一个$k’$使得$Pk’\sqsupset P{q-1}$，也就是$P_{q-1}$的所有公共前后缀的集合(为啥不是$P_q$？因为我们现在正在找的就是$P_q$的啊)，接着看看在这个$k’$的位置上，$P[k’+1]$是否会等于$P[q]$，如果存在这么一个$k’$，那么说明此时$Pq$最长公共前后缀长度就是长度为$k’+1$的$P{k’+1}$。

为什么$P[k’+1]=P[q]$就能说明$P_{k’+1}$就是$P_q$的最长公共前后缀呢？因为首先我们找到了$P_{q-1}$，也就是$P_q$去掉最后一个字符得到的字符串的公共前后缀$P_{k’}$ 图中是$q=|P|$的情况，很明显在$P_{q-1}$中，如果$k’$是$P_{q-1}$的公共前后缀并且$P[k’+1]=P[q]$，则$P_{k’+1}$一定是$P$的公共前后缀，这点对于任意$p\leqslant |P|$都成立

我们一直往后倒着递减$k’$到$0$的位置，如果在这之前都没有任何一个合适的$k’$，那么此时最长公共前后缀长度就是$k’=0$。而计算每上一个$k’$都有一个特殊的技巧，也就是$k’=\pi[k]$(该算法的正确性将会在下文中证明)，我们只需要不停的让$k’=\pi[k],k=k’$，然后判断每一个$k$直到$k=0$为止，这就是函数的第6-7行所做的，它不停的递减$k$，并判断递减后的$k$是否满足$P[k+1]$。接着，如果找到了一个符合条件的$k$，或者一直迭代下去让$k$最终为0，则跳出循环，然后判断$P[k+1]=P[q]$，这点是上文提到过的，如果符合那么就让$k=k+1$(从上图中可以轻松看到$P_q$的最长公共前后缀长度为$k’+1$)，再循环的结束为止，将$k$储存在$\pi[q]$中，代表“$P_q$位置的最长公共前后缀长度为$k$”。

前缀函数的正确性证明

定义1：前后缀关系的传递性

对于字符串$x$, $y$和$z$，如果$x\sqsupset y$且$y\sqsupset z$，则$x\sqsupset z$，也就是说， 后缀关系是传递的 对于字符串$x$, $y$和$z$，如果$x\sqsubset y$且$y\sqsubset z$，则$x\sqsubset z$，也就是说， 前缀关系是传递的

定义2：后缀重叠引理

对于字符串$x$, $y$和$z$，如果$x\sqsupset z$且$y\sqsupset z$，则

1. 有$|x|\gt |y|\implies y\sqsupset x$
2. 有$|x|\lt |y|\implies x\sqsupset y$
3. 有$|x| = |y|\implies x = y$

引理1：前缀函数迭代引理

令$P$是长度为$m$的模式串，$\pi$是$P$的前缀函数，也即$\pi=max({\lbrace k:k\lt m且P_k\sqsupset P_m\rbrace})$，对于$q=1,2,…,m$，设：

有

证明

  这一条就是对于上文中$k’=\pi[k],k=k’$步骤的正确性证明，我们要证明这样得出的$k’$都可以令$P_{k’}\sqsupset P_q$，也就是这个迭代步骤中生成的所有$k$构成了$P_q$的所有公共前后缀的长度的集合。首先我们证明$\pi^\ast[q]\sube\mathcal{S}$，令$u=1$且$k_1=\pi^{(u)}[q]=\pi[q]$(由定义)：

1. 令$u=1$，则$k_1=\pi^{(1)}[q]=\pi[q]$，由$\pi$的定义可以知道$i$一定属于$\mathcal{S}$，即$P_{k_1}\sqsupset P_q$，并且$k_1\lt q$(别忘了看$\pi$的定义)
2. 令$u=2$，有$k_2=\pi^{(2)}[q]=\pi[\pi[q]]=\pi[k_1]$，观察到由$\pi$的定义可知$P_{k_2}\sqsupset P_{k_1}\implies P_{k_2}\sqsupset P_q$(由定义1)，并且$k_2\lt k_1\lt q\implies k_2\lt q$。

由$\lt$的传递性和定义1中给出的$\sqsupset$的传递性归纳可得，对于任意的$k\in\pi^\ast[q]$， 都满足

这意味着$k\in\pi^\ast[q]\implies k\in\mathcal{S}$，也即

  接下来证明$\mathcal{S}\sube\pi^\ast[q]$，我们将会使用反证法证明两个集合的差是空集。首先，假设$\mathcal{S}’=\mathcal{S}-\pi^\ast[q]\neq\phi$，令$j=max(\mathcal{S’})$，我们知道$max(\mathcal{S})=\pi[q]$(依旧是由$\pi$函数的定义直接给出了)，也就是说必然有$j\lt \pi[q]$。因此，令$j’\leqslant \pi[q]$是$\pi^\ast[q]$中大于$j$的最小值($\mathcal{S}’$中$\pi[q]$被删掉了，因此$j$才是$\mathcal{S}’$的最大值，这也是必然的，还是看定义，$max(\mathcal{S})$本身一定属于$\mathcal{S}$，而$max(\mathcal{S})=\pi[q]$，因此$\pi[q]$一定会在$\mathcal{S}-\pi^\ast[q]$时被删掉，这意味着$\pi[q]$一定不属于$\mathcal{S}’$)，因为$j$和$j’$都属于$\mathcal{S}$，因此可以知道$P_j\sqsupset Pq$并且$P{j’}\sqsupset P_q$，又因为$j\lt j’$，所以根据定义2可以知道$Pj\sqsupset P{j’}$，并且我们知道$j$是小于$j’$的最大值，所以必然有$\pi[j’]=j$(因为$j$完美符合了$\pi[j’]$的定义)，又因为$j’\in\pi^\ast[q]$，而从$\pi^\ast[q]$的定义可以知道$\pi[j’]\in\pi^\ast[q]$，即$j\in\pi^\ast[q]$。

为什么$\pi[j’]\in\pi^\ast[q]$？因为定义，$\pi^\ast[q]$中的任意一个$\pi^{(i)}[q]$都等于$\pi[\pi^{(i-1)}[q]]$。因为$j’\in\pi^\ast[q]$，所以可以令$j’=\pi^{(i-1)}[q]$，则$\pi^{(i)}[q]=\pi[j’]$，因为$\pi^{(i)}[q]\in\pi^\ast[q]$，所以$\pi[j’]\in\pi^\ast[q]$

   然而我们在假设中强调了$j\in\mathcal{S’}$，而$\mathcal{S’}=\mathcal{S}-\pi^\ast[q]$，也就是说$\forall_{s\in\mathcal{S’}}(s\notin\pi^\ast[q])$，因此推出矛盾，证明了$\mathcal{S}’$必定是空集，这意味着

(2)和(3)一起，完成了对该引理的证明

引理2

  设$P$是长度为$m$的模式串，$\pi$是$P$的前缀函数，则对于$q=1,2,…,m$，如果$\pi[q]>0$，有$\pi[q]-1\in\pi^\ast[q-1]$,

证明

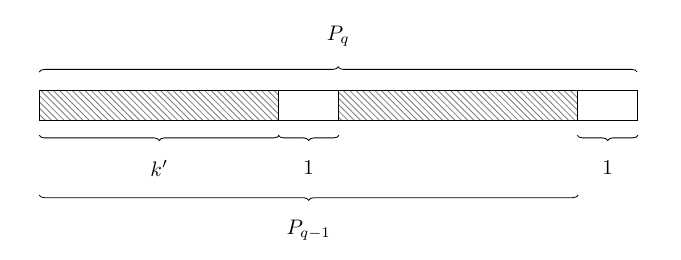
  令$r=\pi[q]>0$，则从$\pi$的定义可以知道$r<q$并且$P_r\sqsupset Pq$，因此可以得知$r-1<q-1$并且$P{r-1}\sqsupset P{q-1}$(可以看上面的那张阴影图，如果$x$是$y$的后缀，那么这两个字符串各去掉末尾的一个字符之后得到的$x’$依然是$y’$的后缀)，应用引理1可以知道，$r-1\in\pi^\ast[q-1]$，也就是$\pi[q]-1\in\pi^\ast[q-1]$，证明完毕   我们可以定义一个$\pi^\ast[q-1]$上的子集$E{q-1}$，该子集包含了所有属于$\pi^\ast[q-1]$并且可以拓展为$P_q$的$k$，也即

其中(5)实际上是把$\pi^\ast[q-1]$的定义展开，而(6)则是把(5)中的后两部分合并(为啥能合并？因为如果$Pk$是$P{q-1}$的后缀，那么如果$P[k+1]=P[q]$，就相当于说明$Pk$和$P{q-1}$的后面一个字符也是相同的，因此算上这个字符之后的$P_{k+1}$依然是$P_q$的后缀)，对于这个集合中的元素来说，只需要把自己递增1，让$Pk$变成$P{k+1}$，就可以变成$Pq$的一个公共前后缀，这个$E{q-1}$的定义将会帮助我们证明算法第6-8行的正确性，它实际上描述的就是我们在开始正确性证明之前的那一段提到过的方法，“找到一个更小的$k$然后给这个$k+1$”

推论1

  设$P$是长度为$m$的模式串，$\pi$是$P$的前缀函数，则对于$q=1,2,…,m$，有：

首先，因为$E{q-1}$的定义是“所有加上1之后就能让$P{k+1}\sqsupset Pq$的$k$的集合”，所以如果$E{q-1}$是空的，那么说明没有任何一个$k$能使得$P_{k+1}\sqsupset Pq$，此时根据定义，$\pi[q]$显然应当等于0。   如果$E{q-1}=\phi$，则需要分两步证明，首先我们证明$\pi[q]\leqslant 1+max(E{q-1})$。令$r+1=\pi[p]$，则$P{r+1}\sqsupset Pq$，因为$r+1=\pi[q]$，所以$r=\pi[q]-1$，这蕴含了两点：1. $r$的值比$\pi[q]$小1，而$\pi[q]$一定小于$q$，因此$r$一定小于$q-1$。2. 根据引理2和之前提到的$P{r+1}\sqsupset Pq$，可以得到$r\in \pi^\ast[q-1]$。综合这两点和之前提到的$P{r+1}=Pq$以及$E{q-1}$的定义可以得到$r\in E{q-1}$，因此$r$一定不大于$E{q-1}$中的最大值，因此$r\leqslant max(E{q-1})$，因为$r=\pi[q]-1$，所以$\pi[q]-1\leqslant max(E{q-1})$，也就是：

  接下来，我们证明$\pi[q]\geqslant 1+max(E{q-1})$。由$E{q-1}$的定义可以知道，对于任意一个$k\in E{q-1}$，都有$P{k+1}\sqsupset Pq$并且$k<q-1\implies k+1<q$，因为$\pi[q]$规定了最大的$k'$使得$P{k’}\sqsupset P_q$，因此$k+1$一定不大于$k’$，也就是$k+1$一定不大于$\pi[q]$(否则$k$不需要加1就有可能是$Pq$的后缀)，又因为$k\in E{q-1}$，所以这蕴含着$E_{q-1}$中的任意一个$k$(包括最大的那个)加上1都不大于$\pi[q]$，即：

(8)和(9)一起，完成了该推论的证明，这一个推论证明了算法第10行递增$k$的正确性

现在可以根据这三条结论来进行前缀函数的正确性证明了，在每次迭代开始前，$k$都等于$\pi[q-1]$，也就是上一次迭代算出的$\pi[q]$，在第一次迭代开始前，第3-4行保证了这点，第12行在每次迭代中都把$\pi[q]$设置为$k$，之后$q$递增1，保证了在下次循环开始前$k=\pi[q-1]$，第6-8行计算$\pi^\ast[q-1]$(因为此时的$k$在本次循环中还没有被更新，依然是$\pi[q-1]$的值)，并算出最大的使得$P[k+1]=P[q]$的$k$的值，也就是$E_{q-1}$的最大值，这一点在引理2中说明，接着在9-11行根据(7)，我们有足够的把握相信，如果$k$找到了，那么就应当让他递增1，如果$k$没有找到，则此时$k$的值一定是0，我们判断$P[k+1]$也就是$P[1]$和$P[q]$是否相等，如果相等则也给$k$递增1，不相等就继续让$k$的值等于0，代表在$P_q$没有任何公共前后缀，注意，如果$k$找到了，那么$P[k+1]$和$P[q]$一定相等，因为这是第6行 while循环的跳出条件，第12行完成对$\pi[q]$的设置，并在第14行返回已经填充好的$\pi$表